算法分析笔记:动态规划

2023年08月19日 2.9k 字大概 13 分钟

动态规划(Dynamic Programming)

1.基本算法思想

同样是由大化小解决，但针对的是分解子问题为非独立的情况。

动态规划算法往往用于解决解的最优化问题。其分解的每一级子结构之间往往有重叠，也就是每次产生的子问题并不完全是全新的问题，问题中可能包含有上一级问题的解。为了提高运算效率，在使用该算法时，一般需要使用表格来记录子问题的解，以方便在向上合并时使用它们。通常来说，其可以按照以下步骤进行设计:

找出最优解性质，并刻画其结构特征;
递归定义最优值;
以自底向上的方式计算出最优值;
根据计算最优值过程中得到的信息，构造最优解。

动态规划算法的基本要素:

最优子结构：如果待解决问题的最优解包含了其子问题的最优解，则称该问题具有最优子结构性质。
重叠子问题：在使用动态规划算法时，每次产生的子问题并不完全是全新的问题，问题中可能包含有上一级问题的解。通过上面所提到的表格记录方法解决，一般可以在多项式时间内完成。
备忘录方法：这是动态规划算法的一种变形。同样使用表格，备忘录方法使用自顶向下的计算方式，其为每个子问题建立记录项，通过检查记录项确定子问题是否已被计算，如果已经计算则直接使用记录项中的值，否则进行计算并记录。

2.算法应用问题

2.1 矩阵连乘(Matrix Chain Multiplication)

2.1.1 问题描述

给定个矩阵，其中与是可乘的()。求这个矩阵的连乘积。

矩阵的乘法是满足结合律的，因此可以修改其运算顺序。我们使用加括号的方式来确定矩阵连乘积的运算顺序。

例如，矩阵连乘积，可以有以下5种运算顺序: 对于不同的运算顺序，由矩阵的乘法运算特性可知，其运算次数其实是不同的。使用和分别表示矩阵那么计算它们矩阵乘积的标准算法代码如下:

void matrix_multiply(int **a, int **b, int ra, int ca, int rb, int cb)  //a,b表示表示矩阵
{
    if(ca != cb)
    {
        error("Unmultiplyable matrix!");
    }
    for(int i = 0; i < ra; i++)
    {
        for(int j = 0; j < cb; j++)
        {
            int sum = a[i][0]*b[0][j];
            for(int k = 1; k < ca; k++ )
            {
                sum += a[i][k]*b[k][j];
            }
            c[i][j] = sum;
        }
    }
}

2.1.2 算法设计

对于矩阵连乘积，将其记为。那么对于一个加括号方式，其运算次数为和的运算次数之积加上它们的运算次数之和。

计算最优值:

设计算所需最少数乘次数为，那么原问题最优解就是的值。对于最优计算顺序是在处断开的情况，可以递归定义为:

其中表示矩阵的列数，且由矩阵乘积结果的性质可以知道：表示矩阵的行数。

对于每一个，都有对应的m[i][j]。我们建立另一个表用于存储的值，这样在获得最优值后，可以递归地由构造出相应的最优解。我们使用递归公式计算矩阵，下面先给出基本代码:

void matrix_chain(int *p, int n, int **m, int **s)
{
    for(int i = 1; i <= n; i++)
    {
        m[i][i] = 0;
    }

    for(int r = 2; r <= n; r++)
    {
        for(int i = 1; i <= n-r+1; i++)
        {
            int j = i+r-1;
            m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];
            s[i][j] = i;
            for(int k = i+1; k < j; k++)
            {
                int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
                if(t < m[i][j])
                {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }
}

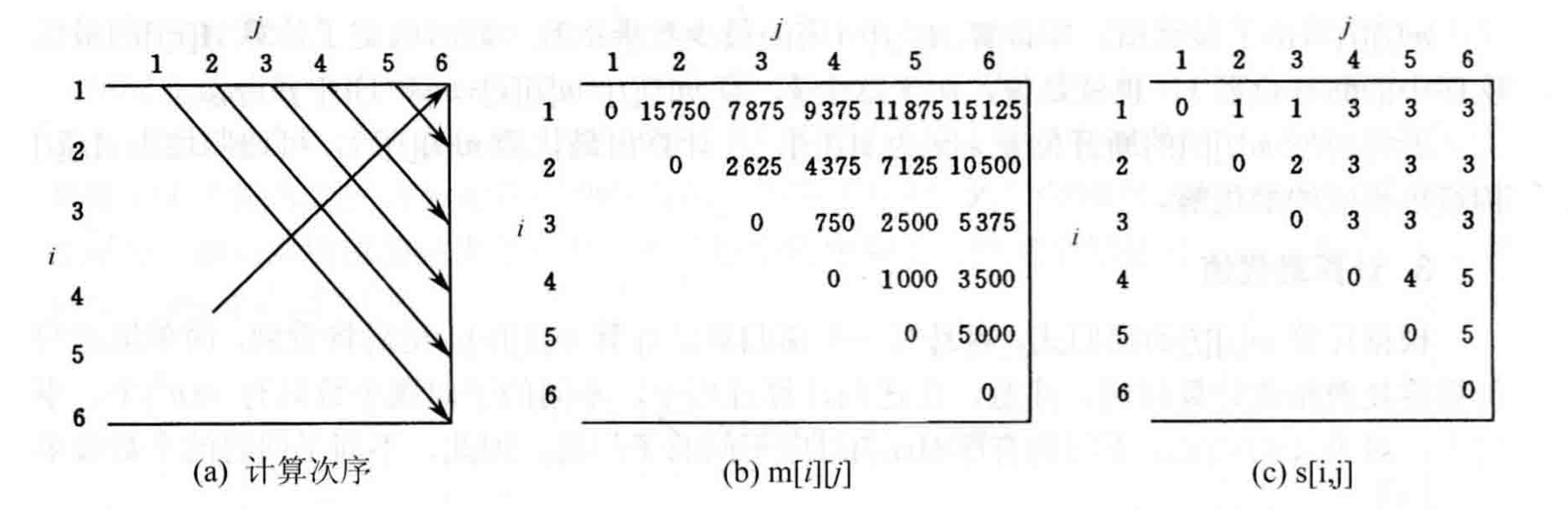
这里给出《计算机算法设计与分析》一书上的样例方便理解。假设需要计算矩阵连乘积。其维数如下:

矩阵	A1	A2	A3	A4	A5	A6
维数	30x35	35x15	15x5	5x10	10x20	20x25

那么其计算顺序以及对应的和矩阵如下:

例如在计算时，递归式如下：

计算过程中我们可以知道在时取到较小值，因此。对矩阵计算完成后，即可获得最优值。

获得最优解:

上面的方法我们仅计算了最少的运算次数，但是还没有得到具体的运算顺序。实际上矩阵所获得的数据就是对应每个计算的顺序信息。

例如记录的信息可以知道计算的最优方式是:。而内部的最优加括号方式又是:。由此递推，最终确定的最优计算顺序。以下是该递推的代码实现:

void Trace_back_matrix(int i, int j, int **s)
{
    if (i == j)
    {
        return;
    }

    Trace_back_matrix(i, s[i][j], s);
    Trace_back_matrix(s[i][j]+1, j, s);
    cout << "Multiply A" << i <<"," <<s[i][j];
    cout << " and A" << s[i][j]+1 << "," << j << endl;
}

通过调用 Trace_back_matrix(1, n, s) 即可获得最优计算顺序。

2.2 最长公共子序列问题(Longest Common Subsequence)

2.2.1 问题描述

给定两个序列和，求和的最长公共子序列。

对于这类问题，我们很明显可以知道其具有最优子结构性质。设序列和的最长公子序列为，则:

若，则，且是和的最长公共子序列;
若，且，则是和的最长公子序列；
若，且，则是和的最长公子序列。

简单理解上述规则，如果在的情况下存在长度大于的公共子序列，则的长度必然大于，也就成为了与的一个长度大于的公共子序列。这很显然和是和的最长公子序列矛盾，因此是和的最长公子序列。同理可证其他情况。

2.2.2 算法设计

在上面提到的三条规则中，可以知道这个问题带有最优子结构性质和子问题重叠性质。其递归方式如下: 1. 如果时，开始找和的最长公共子序列，然后将加入到该子序列尾部; 2. 如果，那就要分别找和的一个最长公子序列，以及和的一个最长公子序列，然后比较两个最长公子序列的长度，取较长的一个即为和的最长公子序列。

我们建立表记录公子序列长度。假如要判断序列;。当或时，空序列就是它们的最长公子序列，此时。上面总结的递归关系式如下:

使用表来记录对应的值是由哪个子问题得到的。我们根据递归关系式获得如下代码:

void LCS_length(int m, int n, char *x, char *y, int **c, int **b)
{
    int i,j;
    //初始化
    for(i = 1; i <= m; i++) 
    {
        c[i][0] = 0;
    }
    for(i = 1; i <= n; i++)
    {
        c[0][i] = 0;
    }

    //构造c和b表
    for(i = 1; i <= m; i++)
    {
        for(j = 1; j <= n; j++)
        {
            if(x[i] == y[j])
            {
                c[i][j] = c[i-1][j-1]+1;
                b[i][j] = 1;
            }
            else if(c[i-1][j] >= c[i][j-1])
            {
                c[i][j] = c[i-1][j];
                b[i][j] = 2;
            }
            else 
            {
                c[i][j] = c[i][j-1];
                b[i][j] = 3;
            }
        }
    }

就是最长公子序列的长度。其函数复杂度为，然后我们根据表递归构造最长公子序列，代码如下:

void LCS(int i, int j, char *x, int **b)
{
    if(i == 0 || j == 0)
    {
        return
    }

    if(b[i][j] == 1)
    {
        LCS(i-1, j-1, x, b);
        cout << x[i];
    }
    else if(b[i][j] == 2)
    {
        LCS(i-1, j, x, b);
    }
    else
    {
        LCS(i, j-1, x, b);
    }
}

该算法的时间复杂度为。

实际上，算法中可以省略数据b，因为在表中，元素c[i][j]往往仅由 $和$ 三个元素决定。因此即使不借助，我们依旧可以知道某个元素是由上面提到的三个元素的哪一个确定的。

2.3 最大字段和(Maximum Subarray Sum)

2.3.1 问题描述

给定由个整数组成的序列，求形如的字段和最大值。

在这个问题中，整数序列允许出现负数，因此如果序列所有整数均为负数时，定义其最大子段和为。例如，当时，最大子段和为。

2.3.2 分治算法解决方法

对于这个问题，我们可以使用分治算法来解决。我们将序列分成长度相等的两段并分别求出它们的最大字段和。其有三种情况:

的最大字段和与的最大字段和相同;
的最大字段和与的最大字段和相同;
的最大字段和为,且，。

对于1、2两种情况，直接进行递归即可。而对于3，我们知道分割点中间两个数一定在最优的序列之中，因此我们可以从分割点向两边扩展，直到序列的两端。这样就可以得到最大字段和。即在中计算出，在中计算出，然后就是的最大字段和。

这样的算法复杂度为。下面给出代码实现:

int Max_sub_sum(int *a, int left, int right)
{
    int sum = 0;
    if (left == right)
    {
        sum = a[left] > 0 ? a[left]:0;
    }
    else 
    {
        int center = (left+right)/2;
        int left_sum = Max_sub_sum(a, left, center);
        int right_sum = Max_sub_sum(a, center+1, right);
        int s1 = 0;
        int lefts = 0;
        for(int i = center; i >= left; i--)
        {
            lefts += a[i];
            if(lefts > s1)
            {
                s1 = lefts;
            }
        }
        int s2 = 0;
        int rights = 0;
        for(int i = center+1; i <= right; i++)
        {
            rights += a[i];
            if(rights > s2)
            {
                s2 = rights;
            }
        }
        sum = s1+s2;
        if(sum < left_sum)
        {
            sum = left_sum;
        }
        if(sum < right_sum)
        {
            sum = right_sum;
        }
    }
    return sum;
}

int Max_sum(int *a, int n)
{
    return Max_sub_sum(a, 1, n);
}

2.3.3 动态规划解决方法

如果,那么所求的最大字段和就是

由此可知，当时，，否则。可以得到其递归式：

该算法时间和空间复杂度都为，得到代码如下:

int Max_sum(int *a, int n)
{
    int sum = 0;
    int b = 0;
    for(int i = 1; i <= n; i++)
    {
        if(b > 0)
        {
            b += a[i];
        }
        else
        {
            b = a[i];
        }
        if(b > sum)
        {
            sum = b;
        }
    }
    return sum;
}

2.4 0-1背包(0-1 Knapsack)

2.4.1 问题描述

有个物品和一个容量为的背包，物品的重量是，其价值为。求解将如何选择物品装入背包可使价值总和最大。

2.4.2 算法设计

设是所给0-1背包问题的一个最优解，则是下面相应子问题的一个最优解：

很显然，该问题具有最有子结构性质。我们设0-1背包问题的最优值为，那么其递归式为:

边界条件如下:

我们使用二维表，基础代码如下:

template <class Type>
void knapsack(int n, Type *w, Type *v, Type c, Type **m)    //动态规划算法
{
    int jMax = min(w[n]-1, c);
    for(int j = 0; j <= jMax; j++)
    {
        m[n][j] = 0;
    }
    for(int j = w[n]; j <= c; j++)
    {
        m[n][j] = v[n];
    }
    for(int i = n-1; i > 1; i--)
    {
        jMax = min(w[i]-1, c);
        for(int j = 0; j <= jMax; j++)
        {
            m[i][j] = m[i+1][j];
        }
        for(int j = w[i]; j <= c; j++)
        {
            m[i][j] = max(m[i+1][j], m[i+1][j-w[i]]+v[i]);
        }
    }
    m[1][c] = m[2][c];
    if(c >= w[1])
    {
        m[1][c] = max(m[1][c], m[2][c-w[1]]+v[1]);
    }
}

template <class Type>
void traceback(Type **m, int w, int w, int c, int n, int x)
{
    for(int i = 1; i < n; i++)
    {
        if(m[i][c] == m[i+1][c])
        {
            x[i] = 0;
        }
        else
        {
            x[i] = 1;
            c -= w[i];
        }
    }
    x[n] = (m[n][c]) ? 1:0;
}

上述代码中，构造出的m[1][c]给出所要求的问题最优值。很显然，算法Knapsack的时间复杂度为，而Traceback的时间复杂度为。